Otimizando carteiras de investimentos com Data Science

As decisões financeiras na prática não são tomadas em ambiente de total certeza com relação a seus resultados. Por essas decisões estarem fundamentalmente voltadas para o futuro, é imprescindível que se introduza a variável incerteza (risco) como um dos mais significativos aspectos do estudo das finanças corporativas. Saber mensurar corretamente o risco e retorno de um negócio, ou seja, saber exatamente com o que está lidando, é uma das principais habilidades que um empreendedor ou um gestor de fundos precisa ter para obter sucesso.

Como então mensuramos o risco? Primeiro precisamos definir uma medida de risco. De maneira geral, medimos o risco pelo quanto de capital precisamos adicionar à nossa posição de risco para termos uma posição aceitável. Por exemplo, suponha que você tenha 1000 reais para investir no mercado de ações e quer ganhar 1 milhão de reais em três anos. O grau de incerteza de obter esse retorno seria ridiculamente alto, (mas teoricamente seria possível, bastando investir no início do dia, na ação que vai dar maior retorno no final dia, e depois trocando para a ação que vai dar maior retorno no final do dia seguinte, sucessivamente) e deveríamos adicionar um capital bastante expressivo nesse investimento para obtermos uma posição aceitável de risco.

Existe várias maneiras de medir um risco de uma carteira de investimentos. Vamos avaliar neste artigo as três mais importantes: Modelo de Markowitz, Valor em Risco (VaR) e Valor em Risco Condicional (CVaR). Mas antes disso, vamos entender o que é ter uma carteira “coerente”. A noção de coerência foi introduzida por Artzner et al e atualmente, é um conceito fundamental relacionado à aceitabilidade de uma medida de risco. A literatura introduz um número de propriedades que são usadas para determinar um medida de risco. As propriedades mais importantes para a medida de risco são

1) Invariância à translação: Se adicionarmos ou subtrairmos uma quantidade certa de nossa carteira, a medida de risco aumenta ou diminui. Matematicamente, se A é o quanto queremos adicionar aos ganhos da carteira X e p a nossa medida de risco, então p(X+A)=p(X)+A. Veja que, se trocarmos instrumentos de renda varável e alocarmos em renda fixa (nessa caso, A é negativo) a carteira diminui o risco no mesmo montante.

2) Subaditividade: Na minha opinião, é a propriedade mais importante ao se avaliar uma medida de risco. Esta medida é intimamente relacionada com o efeito da diversificação do portfólio. A medida do risco total da carteira (conjunto de ativos) é menor ou igual que a medida do risco da soma individual dos ativos da carteira (p(X1)+p(X2)<p(X1+X2)). É o princípio da Teoria Moderno do Portfólio, do grande Markowitz. O VaR falha na subaditivade. Isso significa que, minimizar o VaR não garante que você vá diversificar os investimentos da carteira considerada.

3) Monotonicidade:  Se os ganhos na carteira X são menores que os da carteira Y para todos os cenários possíveis, então o risco na carteira X é menor que na carteira Y (Se X1<X2, então p(X1)<p(X2)). Claro, num portfólio devidamente otimizado, se você quiser arriscar mais, espera que sua possibilidade de ganho seja maior. Markowitz falha na monotonicidade :(.

4) Homogeneidade Positiva: Ao aumentar o tamanho de cada posição da carteira o risco da carteira aumenta em igual proporção (p(bX)=bp(X)), sendo b uma constante). Isso significa que, se você trocar a moeda de uma carteira, ou dobrar seu investimento em cada ação, seu risco aumentará na mesma proporção. Se você aposta 100 reais num jogo de poker e depois triplica a aposta, seu risco triplica também, pois você pode perder (ou ganhar) três vezes mais do que antes.

Pronto, agora vamos entender essas três medidas de risco que comentei anteriormente.

Markowitz, VaR e CVaR. O que são?

São basicamente medidas de riscos, meios de quantificar o risco do investimento. Minimizar essas medidas significa escolher um conjunto de ativos e juntá-los com uma certa proporção específica, de tal forma que a carteira tenha o menor risco possível para um determinado retorno esperado. Vejamos cada uma delas:

Markowitz

Até a década de 50, os modelos para risco e retorno eram em grande parte subjetivos e variavam de investidor para investidor. A partir do desenvolvimento da moderna teoria do portfólio por pesquisadores como Markowitz, Sharp, Black, Scholes entres outros, foi desenvolvido um arcabouço teórico quantitativo com base na teoria econômica neoclássica. O desenvolvimento da teoria do portfólio em 1952 por Markowitz, revolucionou o estudo das finanças, fato que lhe rendeu o prêmio Nobel de economia em 1990.

O principal aspecto da teoria do portfólio é que o risco individual de um ativo é diferente de seu risco na carteira, tornando a diversificação capaz de minimizar o risco não-sistemático dos ativos em conjunto. Com a minimização, é possível escolher a proporção ideal de cada ativo no portfólio, otimizando a relação retorno/risco da carteira de títulos. A figura abaixo representa bem essa ideia: Para mais de 30 ativos, é possível mitigar praticamente todo o risco não-sistemático da carteira. O resto é risco de mercado, crédito, liquidez ou operacional.

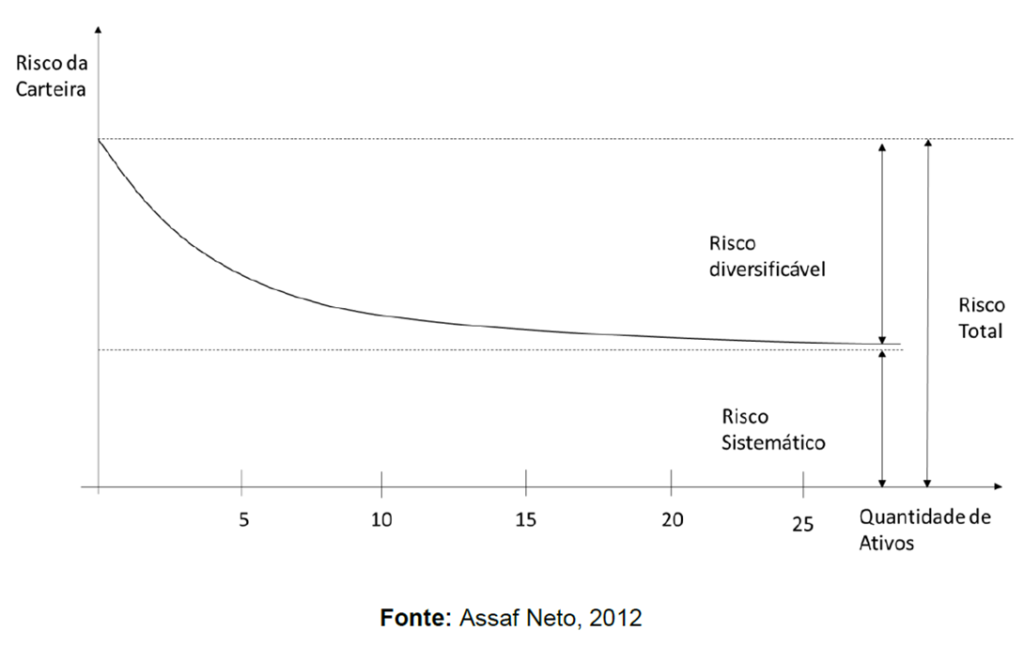
Como exatamente é feita essa diversificação? Suponha duas empresas diretamente concorrentes, A e B, num mercado promissor. Há três possibilidades: A empresa A vence a competição, B vence ou as duas compartilham o mercado. Se você investiu seu dinheiro em uma delas você corre o risco de perder tudo caso a empresa desmorone. Investindo nas duas fará com que você reduza esse risco, pois uma parte certamente vai para a empresa vencedora. E caso as duas percam? Nesse caso, pode ter sido causado por algum fator externo que afetou o mercado, como a pandemia, por exemplo. O modelos de otimização de risco tenta minimizar o risco não-sistemático, via diversificação dos ativos. O risco sistemático não pode ser minimizado.

Como já comentei, essa medida não é coerente, pois não satisfaz a monotonicidade. Outra coisa é que o modelo CAPM (Capital Asset Pricing Models), muito conhecido no mercado financeiro, é uma simplificação da Teoria de Markowitz para tentar reduzir a complexidade computacional do método.

Valor em Risco e Valor em Risco Condicional

Aqui a ideia é entender o risco como o quanto você aceita perder. Muito simples não? Suponha que você vai fazer um investimento de 1000 reais. Seu gerente lhe diz que na carteira X você pode ter um retorno de 300% no ano e que você pode perder no máximo R$ 900 com chance de 5%. O VaR é a perda máxima esperada (não confundir com a perda máxima possível), os R$900,00, e o alfa do VaR é a chance de você perder mais que isso (no exemplo 5%). Minimizar o VaR significa escolher o melhor conjunto de ativos que, com um mesmo retorno, diminua essa perda máxima esperada.

Como já mencionei, o VaR falha na subaditividade. E pior, falha numa propriedade que o pessoal da otimização adora (eu também!), a convexidade. Felizmente, temos uma medida que, além de ser convexa, é coerente. O Valor em risco condicional (CVaR) examina as perdas que excedem o limite do Valor em Risco (VaR). No exemplo que demos da carteira X, isso significa analisar as perdas para 5%, 4%,… de chance e tirar uma média disso. O VaR e o CVaR estão intimamente relacionados e, ao minimizar o CVaR, também levará a uma redução do VaR da carteira. A figura abaixo expressa uma curva normal com as perdas esperadas do Var e CVaR e as probabilidades esperadas.

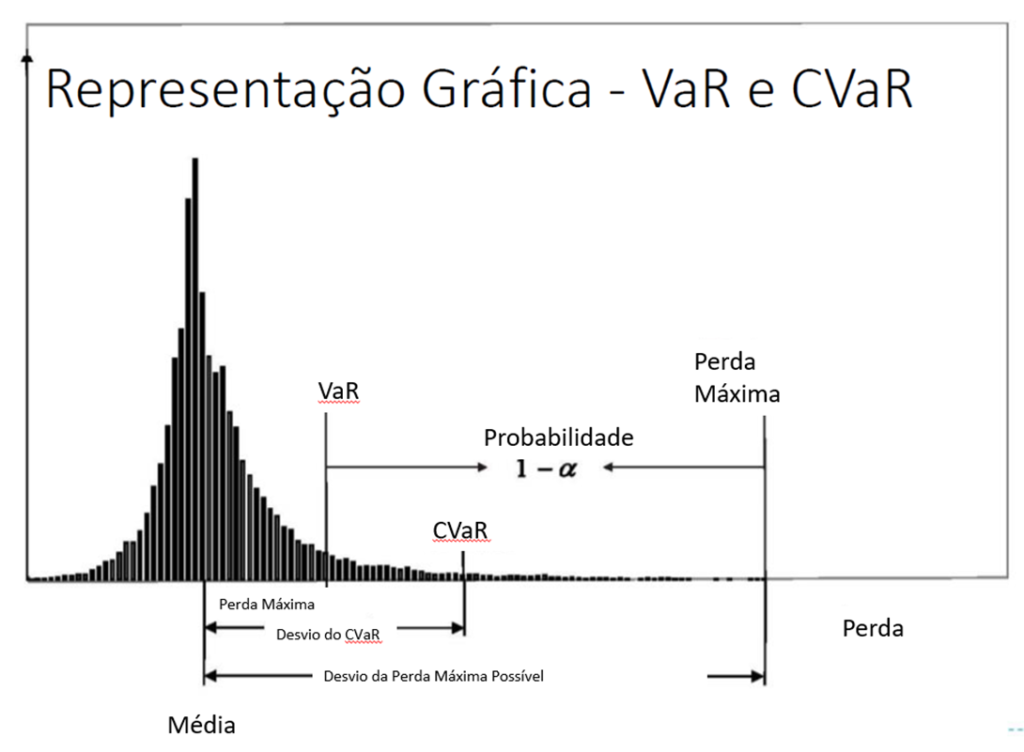
Resumindo de maneira matemática o que explicamos:

1. O VaR tenta resumir em um único número, a perda máxima esperada dentro de um certo prazo com um certo grau de confiança estatística
   

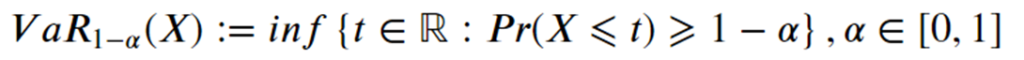
2. O CVaR pode ser definido como a esperança condicional de perdas das carteiras superiores ao VaR:

O problema de otimização

Resolver um problema de otimização é buscar a melhor utilização de recursos e processos (técnico, econômico, social ou político), através de aplicação de modelos matemáticos, visando otimizar a satisfação (utilidade) do usuário. Compreende o problema de alocar recursos escassos para realização de atividades e cita alguns exemplos de técnicas particulares da otimização:

1. Programação Linear: aplicada em áreas relativas à alocação de pessoal, mistura de materiais, distribuição, transporte, etc.;
2. Programação Dinâmica: utilizada principalmente para problemas de otimização combinatória, tem aplicações em a áreas como planejamento de despesas de publicidade, distribuição do esforço de vendas e programação de produção;
3. Teoria das Filas: área que estuda analisar a formação de filas, é aplicada na solução de problemas relativos a congestionamento de tráfego, máquinas de serviços sujeitas à quebra, determinação do nível de uma força de serviço, etc.;
4. Programação Não Linear: é um modelo matemático onde a função objetivo, as restrições ou ambas, apresentam não linearidade em seus coeficientes.

Na área de investimentos, é utilizado métodos de programação linear ou não-linear para maximizar ou minimizar a função objetivo. Um modelo de otimização para investimentos envolve os seguintes conceitos:

1. Função objetivo: Representa o principal objetivo do tomador de decisão. No modelo de VaR é dada pela minimização da perda máxima esperada ou maximização do retorno da carteira. É uma função multi-objetivo, então a solução é uma curva, a fronteira eficiente, com a perda mínima para cada retorno.
2. Restrições: Diz o que é possível ou não fazer e quais são as limitações dos recursos ou atividades que estão associados ao modelo. No modelo em questão, as limitações são: a participação dos ativos precisa ser maior que zero, a soma de as participações deve ser igual a 1, e colocar um retorno mínimo exigido pelo cliente, ou um risco máximo, dependendo do objetivo do investido.
3. Variáveis de decisão: variáveis que podem ser controladas pelo tomador de decisão. No modelo correspondem à participação ao peso de cada ativo no portfólio.

Vejamos o modelo para o problema de minimização do CVaR. A partir de uma série da manipulações matemáticas, Rockafellar e Uryasev (2000) reescreve o cálculo do CVaR em termos de uma função, dada por

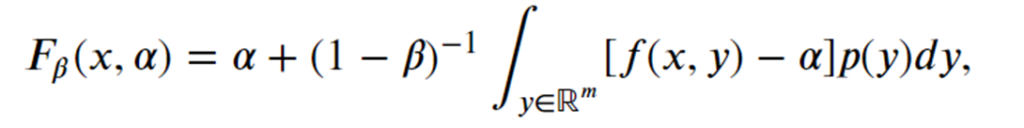
Para o caso de valores discretos, a equação acima pode ser reescrita como:

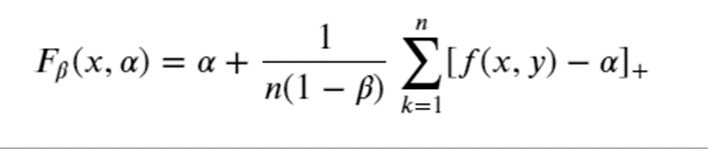
Dessa maneira, Rockafellar e Uryasev (2000) usa a função F linear para definir a forma para a otimização de uma carteira de ações utilizando o CVaR como medida de risco:

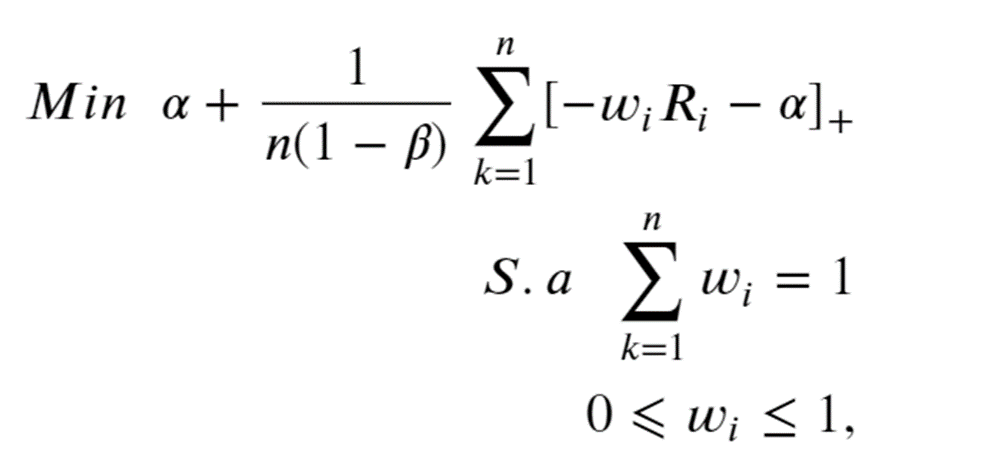
onde n é o tamanho da amostra e w_i a proporção de cada ativo na carteira.

Resultados na Prática

Vamos avaliar o modelo para otimização do VaR e CVaR utilizando 30 ações da bolsa de valores do Brasil. Utilizaremos como histórico o retorno das ações desde o começo da pandemia (para evitar envasamento histórico de análise, já que a pandemia alterou a dinâmica do mercado de ações).

Agora, utilizando a biblioteca de otimização scipy do python, conjuntamente com bibliotecas que fazem interpretações das integrais, traduzimos a função objetivo e as restrições para o código e, usando como técnica de otimização linear o simplex revisado, construímos a fronteira fronteira eficiente para o VaR e CVaR.

Os gráficos abaixo expressam o retorno para cada valor em risco considerado. Devido ao fato da otimização do VaR não ser convexa, a fronteira eficiente da otimização com o VaR tem um comportamento mais “caótico” comparada à otimização com o CVaR, que tem um comportamento mais suave.

O CVaR varia de 10% a 30% com retorno de 6% a 16 % do valor investido. Essa abordagem também levou a uma redução no VaR, uma vez que é um fator envolvido no processo de minimização do CVaR. Vale lembra que o CVaR é uma medida mais conservadora, o que explica um risco maior do CVaR, dado o mesmo retorno, que o VaR.

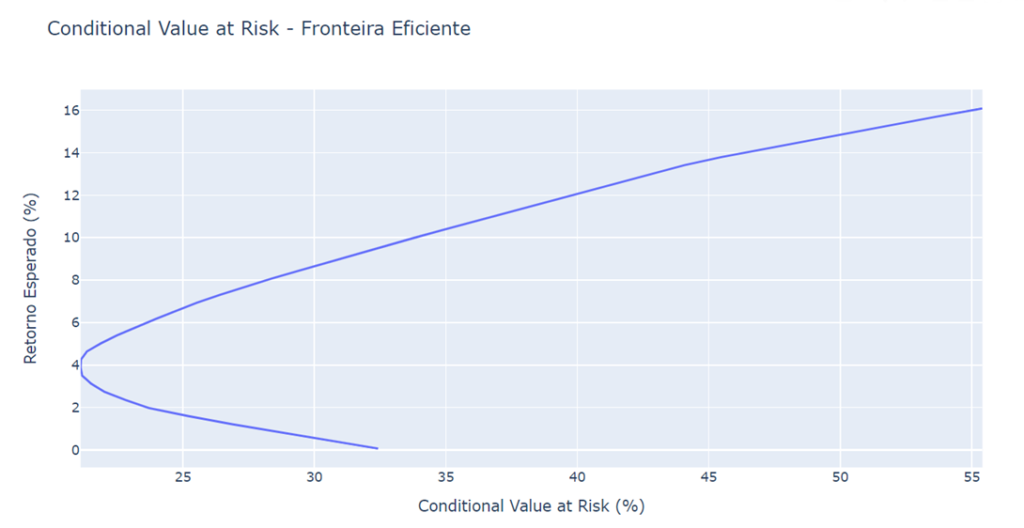
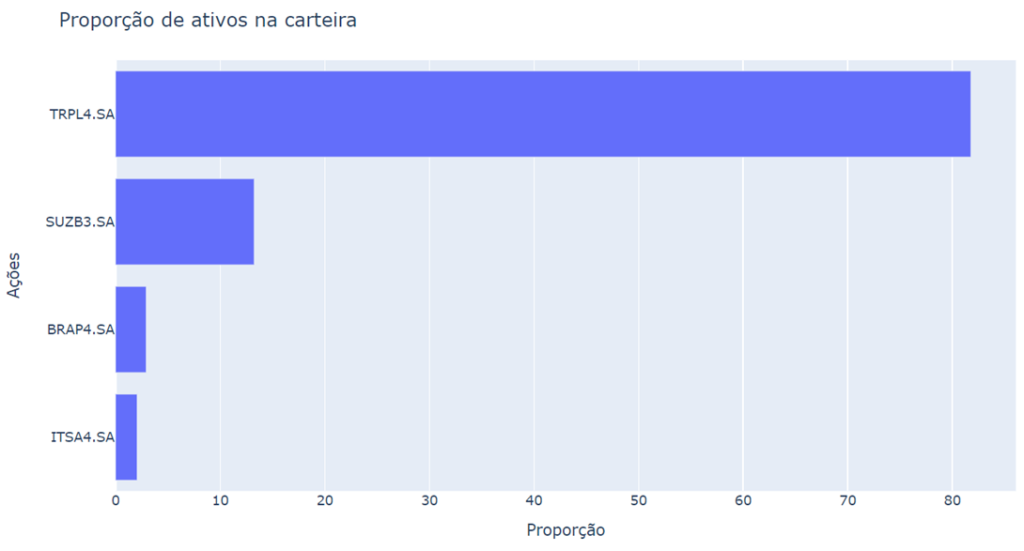
O gráfico de área abaixo expressa a proporção de ativos na carteira para cada valor em risco considerado.

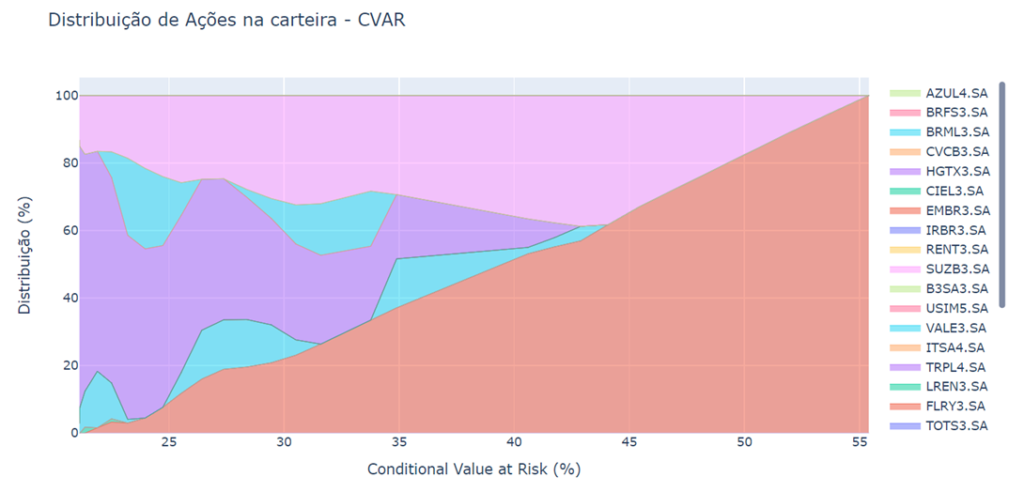
O resultado final é, para um dado valor em risco, as ações que devo investir e em qual proporção, para o meu portfólio ótimo. Exemplo, caso eu queira assumir um CVar de 20%, o conjunto de ativos que me trariam o melhor retorno seria:

Trans Paulista (TRPL4) – 82%, Suzano Papel (SUZB3) – 13%, Bradespar (BRAP4) – 3%,

Itausa (ITSA4) – 2%.

Backtest

Para validarmos o modelo, é importante fazer uma análise de backtest. O objetivo do backtest é analisar quais seriam os resultados de um carteira ótima criada num período anterior ao atual, verificando a evolução do retorno da carteira desde o instante em que ela foi criada, até o instante atual.

Analisando a evolução do retorno para 5 níveis de risco diferentes, podemos notar o seguinte:

1. Quanto maior o risco, mais volátil será a carteira;
2. Em nenhum dos casos a perda ultrapassou a perda máxima esperada. Exemplo, para um CVaR de 20%, o ponto mínimo foi de 4600 (8% de perda);
3. Para esse caso em particular, o CVaR de 25% acabou perfomando melhor, inclusive gerando um retorno de 6,72% durante o período avaliado (dentro do esperado ao verificar a fronteira eficiente).
   

Bônus: Minimizando medidas de risco usando a Teoria da Evolução

O que a Teoria da Evolução tem a ver com tudo isso que fizemos? Bom, se você entendeu a matemática da função objetivo, sabe que essas fórmulas do VaR e CVaR são bastante “cabeludas”. Existem algoritmos de otimização específicos para cada um dos problemas (programação linear para o CVaR, programação quadrática para Markowitz e algum método de otimização não-convexa para o VaR), mas não que minimiza os três com o mesmo método. Para minimizar o risco das três carteiras que estudamos, podemos usar um algoritmo genético da inteligência artificial que é baseado na Teoria de Darwin, o Differential Evolution (DE). O DE tem se apresentado como um simples, mas poderoso algoritmo de otimização numérica para busca da solução ótima global, sendo aplicado com sucesso na solução de vários problemas de otimização complexa.

Para otimizar um portfólio utilizando o algoritmo DE, melhoramos iterativamente uma solução candidata de uma população gerada de carteiras, c1,…,c𝑖, 𝑖 = 1,…, n onde cada carteira contém N elementos e representa as variáveis objetivas, ou seja, os retornos históricos dos ativos do portfólio. A DE visa otimizar o trade-off entre risco e retorno, em vez de minimizar o risco de um determinado retorno específico, ou seja, teremos uma avaliação de retorno para diversos riscos possíveis. Isso é o que chamamos de fronteira eficiente da carteira.

A ideia básica do DE é produzir uma nova solução para cada carteira atual, onde a nova solução é uma combinação de quatro soluções atuais na população. Funciona da seguinte maneira:

1) Selecione uma carteira (c0) da população atual, que será nossa carteira-pai. Em seguida, selecione aleatoriamente três carteiras diferentes, usando um deles como uma carteira-base e adicione a diferença ponderada das outras duas para construir uma nova solução,

cm=c1+F*(c2-c3),

onde 𝐹 é um fator de mutação entre 0 e 1 que controla a taxa na qual a população de carteiras evolui. A solução dessa fórmula, cm, será nossa carteira-mutante.

2) Agora, realizamos um cruzamento entre a carteira-pai e a carteira-mutante. Cada elemento na carteira-filha será determinado por uma taxa de crossover (CR – razão de cruzamento) definida pelo usuário, onde 𝐶𝑅 está entre 0 e 1, e um número gerado pseudo-aleatório ε. O cruzamento controla a fração de valores de parâmetros copiados da carteira-mutante, de modo que, se o número gerado for menor que a razão de cruzamento, a carteira-filho herdará o elemento 𝑗 da carteira-pai. Da mesma forma, se o número gerado for maior ou igual à razão de cruzamento, a carteira-filho herdará o elemento 𝑗 da carteira-mutante. A figura abaixo dá a visualização gráfico disso:

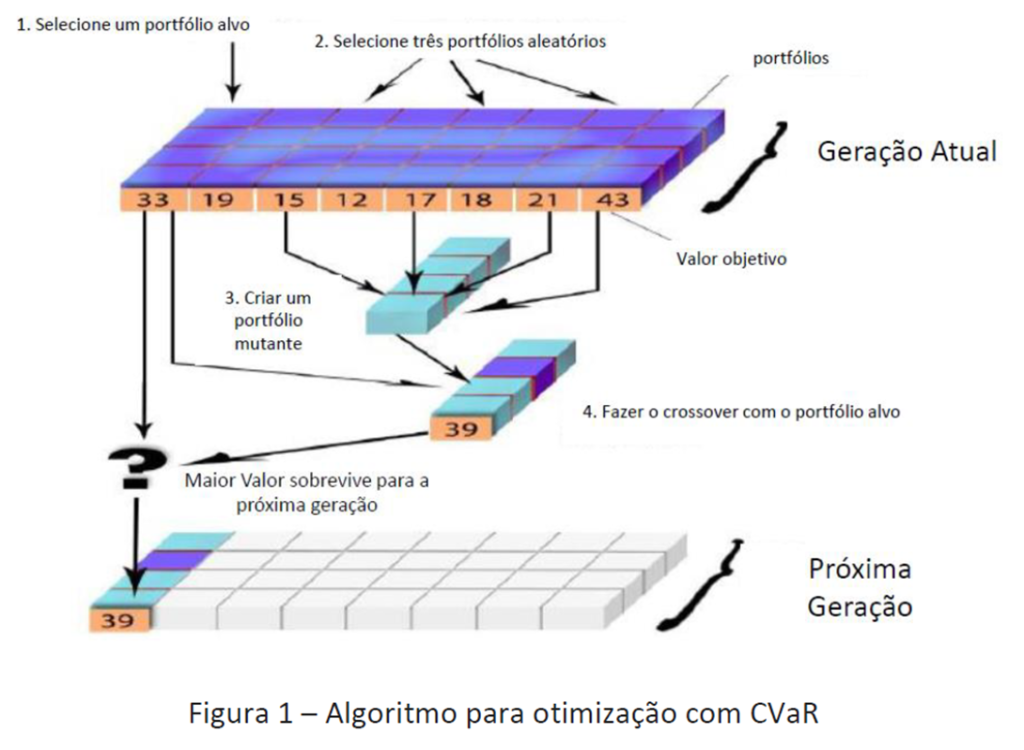
3) Há ainda algumas medidas para evitar que os ativos saiam do espaço viável de soluções, pois não podemos ter carteiras com ativos que, somados, dão pesos maiores que 100%. Para resolver isso, lembre-se de normalizar todas as carteiras de sua população.

Hora da prática

Apresentamos aqui a escolha de parâmetros para o algoritmo DE e comparamos seus resultados com outras técnicas de otimização. Consideramos uma carteira composta apenas por ações e assumimos que os retornos diários dos registros são normalmente distribuídos. Com relação aos dados, vamos utilizar 25 ações da BM&Fbovespa, usando cotações históricas diárias de 5 anos. Além disso, vamos assumir que há 252 dias de negociação por ano e, assim, escalaremos os retornos proporcionalmente ao tempo. Para a programação dos algoritmos, eu utilizei o software Matlab.

Primeiro veremos a medida de Markowitz. Para o caso da volatilidade, na figura abaixo fizemos uma comparação entre o método de otimização quadrática e a evolução diferencial, com parâmetros N = 25, F = 0,5, CR = 0,7 e ε = 1%. A fronteira da carteira indica o quanto de risco você você assume para cada retorno esperado. Podemos ver que o retorno esperado ideal sobre o investimento varia de 16% a 35%, e a volatilidade de 13% a 22%, ou seja, a tendência de movimento da carteira. Além disso, ao analisar os retornos e riscos dos ativos individualmente, vemos que a diversificação representa um risco menor e, ao mesmo tempo, produz um retorno maior, onde cada portfólio ideal fica ao longo da fronteira eficiente.

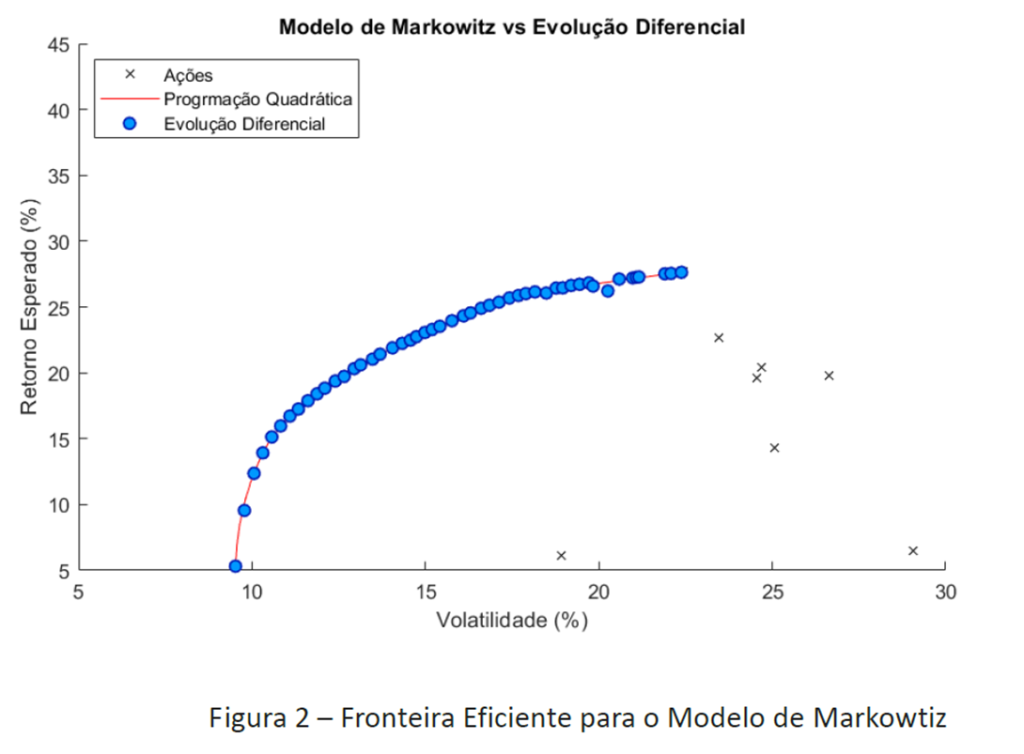
Para mostrar que o DE pode lidar com qualquer medida de risco, usamos a abordagem de R. T Rockafellar e S. Uryasev para minimizar o CVaR comparando as soluções do algoritmo DE com o de programação linear. Usamos aqui a mesma suposição do último caso e aproximamos os retornos. Em seguida, vamos otimizar o CVaR usando os mesmos parâmetros de antes. Esses valores foram escolhidos pois são que oferecem melhor acurácia em um tempo admissível (Dependendo dos parâmetros que você escolhe, pode ficar até dias esperando sua carteira “evoluir”). Temos então a seguinte fronteira:

O CVaR varia de 30 % a 100 % do valor investido, que é a proporção média de um capital de investidores que será perdido para o nível de probabilidade de perda de 5%. Essa abordagem também levou a uma redução no VaR, uma vez que é um fator envolvido no processo de minimização do CVaR. Para o VaR, na figura abaixo, vemos que o valor varia de 22% a 70%. De qualquer forma, vemos que o DE está na fronteira eficiente e podemos confirmar que as soluções são as mesmas para os métodos específicos de cada método, investigando novamente a distribuição do peso do portfólio.

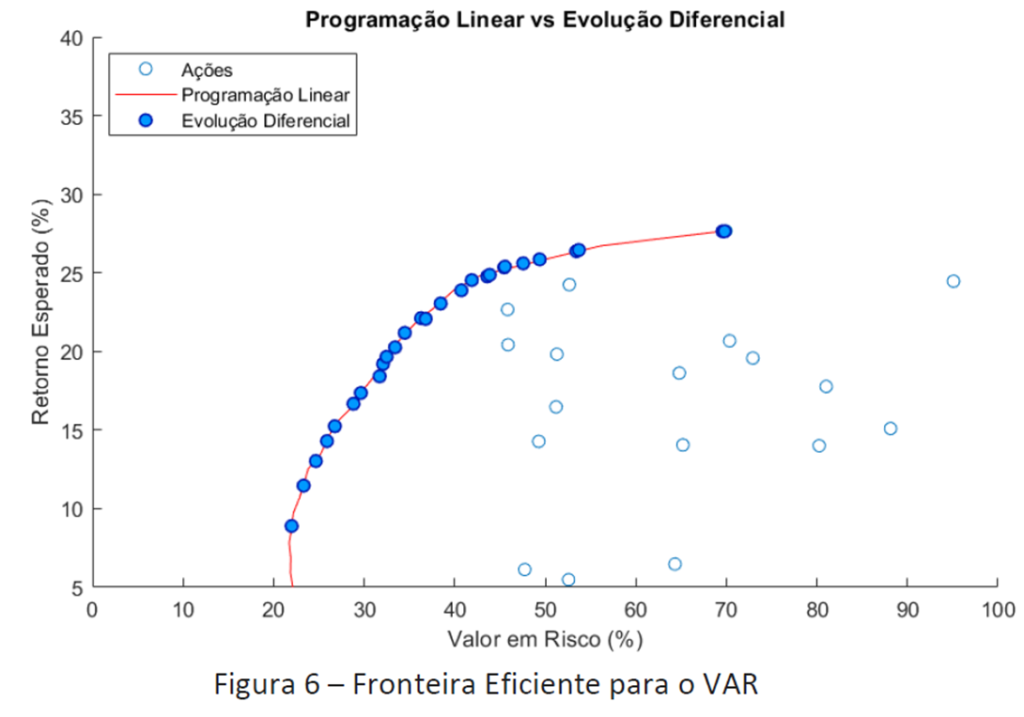
Percebeu que a fronteira do VaR é um pouco “deformada”? Isso é justamente devido ao fato de não termos aqui aquela propriedade da convexidade envolvida.

Bom, agora vamos para o que importa. Quais os ativos e quanto investir em cada um para formar uma carteira eficiente evoluída? vEis os resultados de acordo com Markowitz e o CVaR:

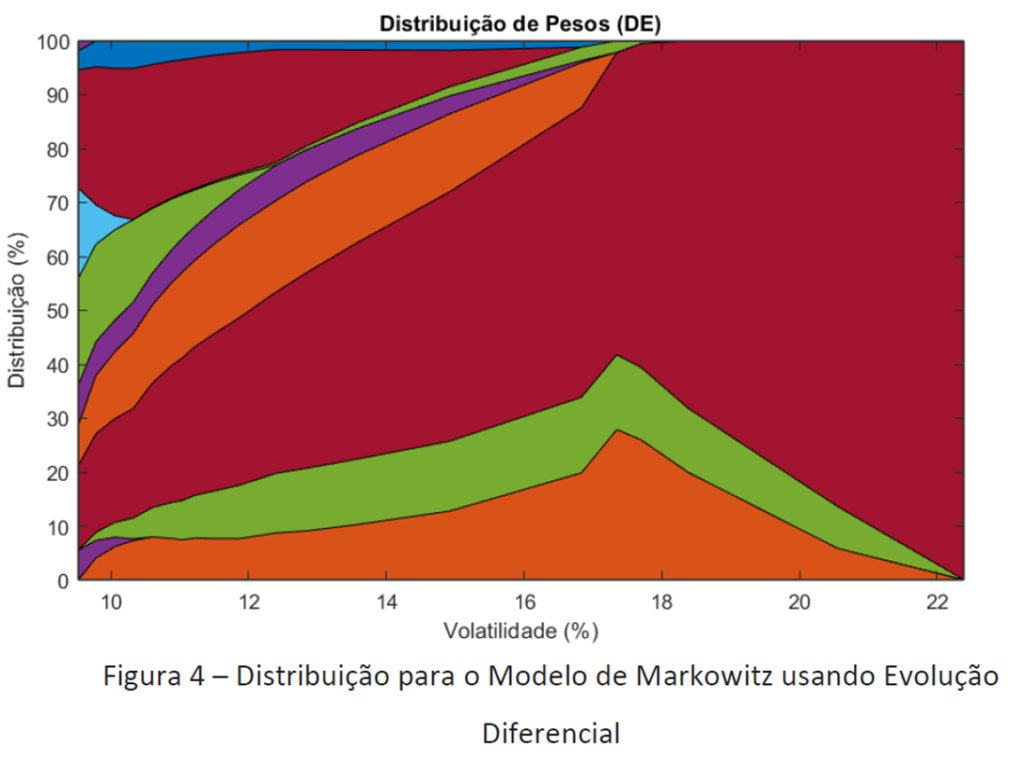
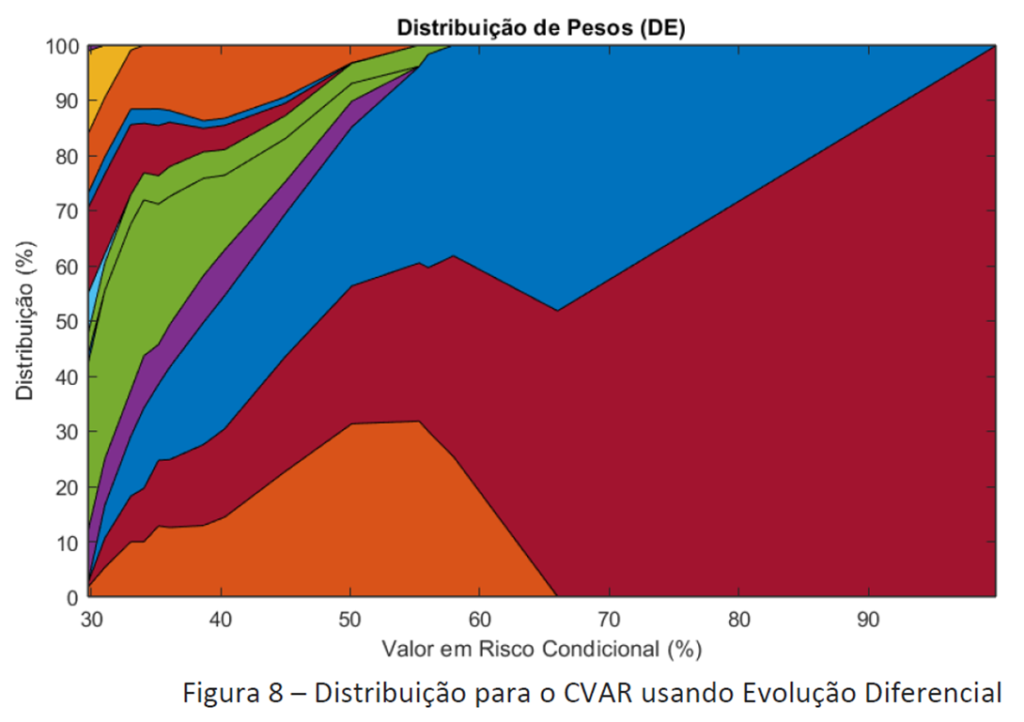
Nesses gráficos, para cada Volatilidade (Risco) e CVaR, temos uma proporção de ativos diferentes. Por exemplo, para termos um CVaR de 65%, temos que investir 27% na ITUB4 28% na EMBR3 e 45% na B3SA3.

Concluindo, mostramos como fazer uma carteira eficiente e também verificamos que a Evolução Diferencial é um algoritmo de busca robusto que pode ser aplicado ao problema do minimização de uma carteira. Com relação ao tempo médio de execução do algoritmo, outras estratégias no processo de mutação poderiam ser úteis no processo de obtenção de um tempo mais rápido.

#cienciadedados #pesquisaoperacional #financas