Utilizando Aprendizado de Máquina para predizer falhas na Ferrovia

INTRODUÇÃO

Quando o trilho atinge certas temperaturas muito baixas, o risco de acidentes de diversos portes aumenta significativamente, portanto é uma variável constantemente monitorada. Com o objetivo de aumentar a segurança operacional e reduzir custos, surgiu a hipótese de implementar um modelo preditivo que deve ser capaz de capturar padrões nas temperaturas enviadas pelo termômetro do trilho e estimar a probabilidade de que nas próximas 12 horas, ocorra uma temperatura crítica no trilho, dessa forma é possível emitir avisos de segurança e enviar veículos batedores para avaliar a condição do trilho preventivamente. A ideia inicial é coletar o histórico de medições de um termômetro específico e ajustar um algoritmo de aprendizado de máquina aos seus dados históricos.

Se trata de uma demanda onde não há variável resposta e nem variáveis preditoras. As únicas informações que estavam no histórico de dados eram os registros de data / hora e a temperatura do trilho medida em cada instante. Então deverá ser criada uma variável resposta para tratar o problema como uma tarefa de classificação binária, e um forte trabalho de engenharia de variáveis, criando diversos preditores como médias móveis, desvios padrões móveis e informações de momentos passados da temperatura do trilho.

O problema no trilho devido à baixa temperatura é um evento extremamente raro. Basicamente em 99% dos dados observados não ocorrem temperaturas críticas, portanto foi necessário recorrer a uma abordagem algorítmica para trabalhar esse desequilíbrio entre os eventos, para que o algoritmo de aprendizado de máquina possa capturar da melhor forma os padrões nas mudanças da temperatura que levam a ocorrência de uma temperatura crítica nas próximas 12 horas bem como o padrões que levam a não ocorrência de uma temperatura crítica nas próximas 12 horas.

Dentre os algoritmos de aprendizado de máquina testados na modelagem preditiva, a regressão logística com a adição de restrições na sua função objetivo foi o algoritmo que melhor performou, chegando a praticamente zerar os falsos negativos, que são os mais críticos para este contexto, já que, é mais custoso o algoritmo informar que não vai ocorrer a temperatura crítica e ela ocorrer (falso negativo) do que informar que vai ocorrer a temperatura crítica e não ocorrer (falso positivo).

DIAGNÓSTICO

1. Obtendo os dados

Os dados utilizados para ajuste do modelo preditivo foram as medições da temperatura do trilho de uma determinada região em Minas Gerais, de janeiro/2017 até março/2019, contendo 24.105 medições observadas, que são enviadas do termômetro do trilho diretamente ao banco de dados da empresa, em uma interação máquina vs máquina.

Figura 1 – Amostra do histórico de temperaturas enviadas pelo termômetro do trilho

As medições são enviadas pelo termômetro, geralmente, em intervalos de 15 minutos. Então,

para manter um histórico de medições com intervalos equidistantes, os dados foram agregados por hora, e ao agregar, foram tomadas estatísticas descritivas da temperatura em cada hora, para auxiliar na análise exploratória dos dados bem como ajudar no processo de criação de variáveis preditoras.

Figura 2 – Amostra do histórico de temperaturas agrupados por data e  hora

• Análise Exploratória dos Dados

Conforme definido por Pinheiro, Cunha, Carvajal e Gomes (2009), analisar dados é identificar comportamentos médios e comportamentos discrepantes, comparar comportamentos e investigar a interdependência entre variáveis. Portanto, a análise exploratória de dados é uma forma eficiente de resumir dados e ajudar a revelar informações contidas neles, e assim utilizar o conhecimento para auxílio a tomada de decisão.

A análise exploratória de dados trata-se de um conjunto de técnicas que nos ajudam a fazer uma sondagem dos dados, ou seja, tomar um primeiro contato com a informação disponível.

Através de um histograma, é possível visualizar a distribuição das temperaturas médias em cada uma das vinte e quatro horas do dia, durante janeiro de 2017 até março de 2019, que é o histórico de dados disponível. O histograma é uma distribuição das frequências dos dados, semelhante a um gráfico de barras, porém cada barra representa a frequência de um intervalo de valores.

             Figura 3 – Distribuição das temperaturas médias e estatísticas descritivas

Por motivo de sigilo de informações a temperatura limiar exata para ser considerada crítica será omitada, mas para fins didáticos e de forma a não distorcer o presente artigo, uma temperatura bastante aproximada será utilizada. Será assumido que, se o trilho atingir uma temperatura menor ou igual a seis graus, será considerado estado crítico. E como é de se esperar, esse padrão ocorre com maior frequência no inverno.

Em um gráfico sequencial, com as temperaturas ordenadas ao longo do tempo, fica mais intuitivo visualizar quando ocorrem as temperaturas críticas com maior frequência.

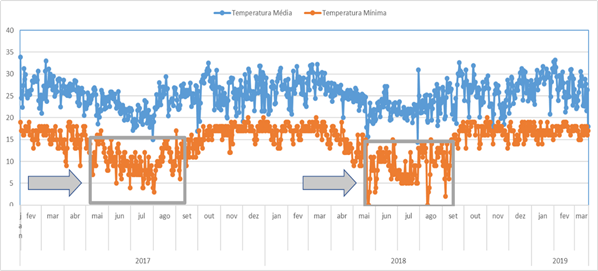
        Figura 4 –Evolução das temperaturas médias e mínimas ao longo do histórico de dados

Também foram exploradas, as variações das temperaturas mínimas dentro de cada mês.

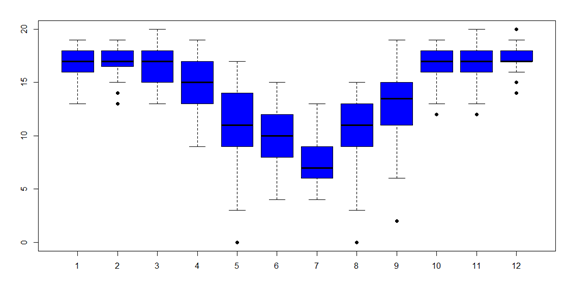
              Figura 5 – Variações das temperaturas mínimas intra mês

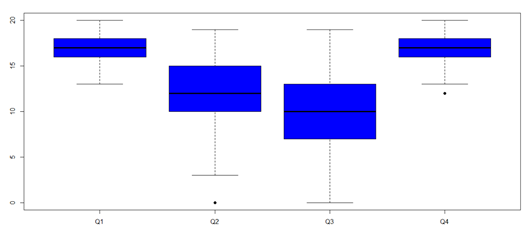
Fica claro que em alguns meses a temperatura apresenta comportamento mais homogênio, já em alguns ocorrem grande variabilidade. O mês de maio é bastante crítico, pois seu boxplot na figura 5, a dispersão nas temperaturas é grande, ocorrem desde temperaturas críticas (abaixo de seis graus) até temperaturas mais elevadas. Também foram analisadas as distribuições das temperaturas mínimas dentro dos trimestres.

Modelando a relação entre as temperaturas mínimas e os trimestres através de uma regressão de mínimos quadrados e tomando o primeiro trimestre (Q1) como nível de referência, temos que, o segundo trimestre (Q2) apresenta, em média, temperaturas 4,72 graus menores. O terceiro trimestre (Q3) apresenta, em média, temperaturas 6,46 graus menores. E o quarto trimestre (Q4) não apresentou diferenças significativas em suas temperaturas mínimas quando comparado ao primeiro trimestre.

Também foi explorada a relação entre as temperaturas médias e a hora do dia durante o período histórico.

          Figura 7 – Relação entre as temperaturas médias por hora do dia

A temperatura média apresenta uma relação não linear com as horas do dia, as temperaturas mínimas ocorrem por volta das seis da manhã e as máximas por volta das 15 horas. A curva de vermelho na figura 7 é um ajuste polinomial da relação entre as duas variáveis.

Além disso, também foi avaliado se existe correlação entre a temperatura do trilho com ela própria em diferentes instantes temporais. Para isso, um correlograma foi utilizado. Um correlograma é um gráfico de barras, onde cada barra corresponde ao coeficiente de correlação linear da variável com ela mesma defasada no tempo.

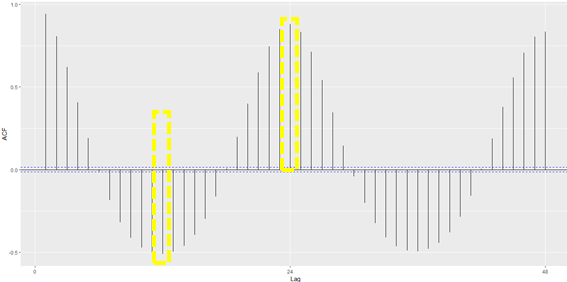
                             Figura 8 – Correlograma da temperatura do trilho

Através do correlograma da figura 8, vemos que a temperatura no instante zero, tem uma alta correlação negativa com ela mesma no instante doze (primeira barra amarela da esquerda pra direita) e  outra forte correlação com ela mesma, porém positiva, no instante vinte e quatro (segunda barra amarela da esquerda para direita). Ou seja, existe um forte padrão entre a temperatura medida em um instante atual com as temperaturas medidas 12 e 24 horas atrás. Isso é ótimo, pois a ideia do modelo é predizer a ocorrência de uma temperatura crítica (abaixo de seis graus) com doze horas de antecedência.

A covariância de uma variável ordenada ao longo do tempo com ela mesma em um período temporal diferente fica:

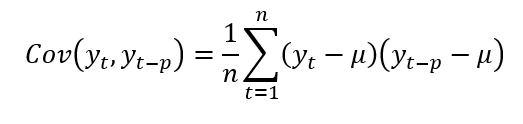
Onde Y_t é a variável em seu instante atual, y_t-p é a variável defasada em p períodos temporais, µ é a média da variável e n é a quantidade de observações.

Para obter o coeficiente de correlação linear deve-se normalizar o produto interno no numerador da equação pelo raiz quadrada do produto entre a variância da variável no período t pela variância da variável no período t-p.

2) Engenharia de Variáveis

Após compreender o comportamento da temperatura do trilho através das análises exploratórias, seguiu-se para próxima etapa que foi a engenharia de variáveis. A engenharia de variáveis, ou engenharia de atributos, ou feature engineering, é a arte de criar novas variáveis a partir das variáveis disponíveis.

De início foram criadas médias móveis de diferentes ordens. Médias móveis de ordem grande reagem de forma mais lenta as variações recentes na temperatura, enquanto médias móveis de ordem menor reagem mais rapidamente as variações na temperatura.

A média móvel de ordem n da temperatura do trilho pode ser obtida por:

Onde y_t é a temperatura no instante t e n é a ordem da média móvel. O nome média móvel é utilizado porque, a cada período, a observação mais antiga é substituída pela mais recente, calculando-se uma média nova.

Pelo gráfico exibido na figura 9 é possível visualizar que quando uma média móvel muda de nível com a outra, é indicativo de mudança na direção da temperatura, ou seja, é uma forma do algoritmo “aprender” quando a temperatura deixa de subir para diminuir, e vice-versa.

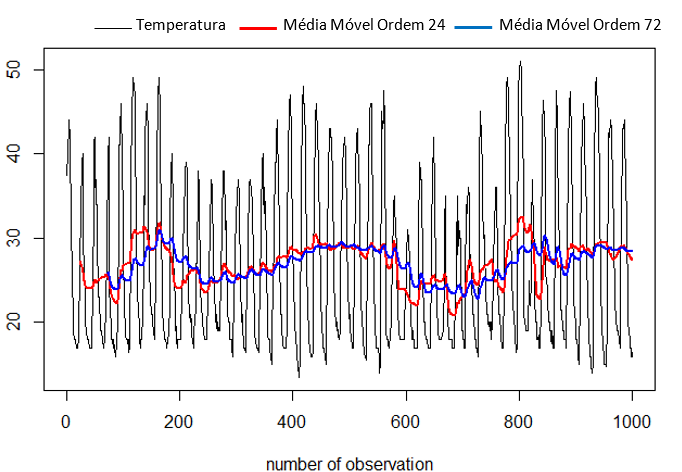
        Figura 9 – Média móvel de ordem 24 vs média móvel de ordem 72

Conforme identificado na figura 4, as temperaturas críticas ocorrem com maior frequência nos meses de maio, junho, julho e agosto. Portanto, foi criada uma variável binária para capturar o padrão desse período de inverno. Nos registros cujo mês for igual a maio, junho, julho, julho ou agosto a variável assume o valor 1(sim), caso contrário, assume o valor 0(não).

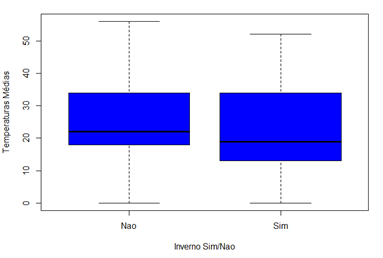
       Figura 10 – Distribuição das temperaturas de acordo com a nova variável binária

Observa-se claramente que a mediana das temperaturas no inverno é menor quando comparada a mediana das temperaturas quando não é inverno. E mediante uma ANOVA, comprovou-se que a diferença é estatisticamente diferente (Pr(>F) ≅ 0).

O próximo passo foi criar a variável resposta. Para isso o seguinte looping foi desenvolvido:

               Figura 11 – Looping em linguagem R para criar a variável resposta binária

A lógica do looping é percorrer da linha 1 até a n-ésima do conjunto de dados, se a i-ésima temperatura for menor ou igual a seis graus, então a linha de posição i – 12 recebe o valor

Temperatura_Critica, caso contrário, recebe o valor Temperatura_Nao_Critica. A linha de posição i – 12 que recebe o valor pois a ideia é registrar se 12 horas após a medição de posição i – 12 ocorreu uma temperatura crítica.

Ainda foram criadas outras variáveis preditoras. Por exemplo, desvio padrão móvel de ordem 2 e 12. Um desvio padrão móvel pode ser obtido pela equação:

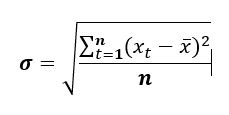
Onde n é a ordem do desvio padrão móvel.

Na figura 12, é apresentada uma função de densidade para medir o quão bem os desvios padrões móveis separam as classes da variável resposta, ou seja, o quão diferente é o padrão das variações das preditoras criadas quando há temperatura crítica e quando não há.

Quanto menos intersecção as funções de densidade tiverem, melhor elas separam os eventos, e consequentemente, contribuirão para a aprendizagem do algoritmo.

Figura 12 – Densidade das variáveis criadas para Temperaturas Críticas e Não Críticas

Também foram criadas variáveis de potência maior da variável hora, como hora ao quadrado e hora ao cubo. Com o objetivo de capturar o comportamento polinomial apresentado na figura 7.

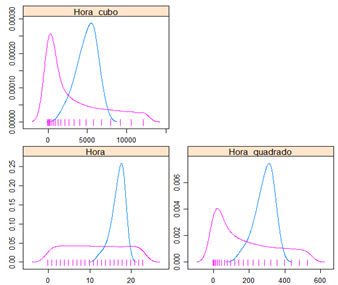
Figura 13 – Densidade das variáveis criadas para Hora em relação as Temperaturas Críticas e Não Críticas

Com o objetivo de capturar mais informações de instantes passado da temperatura, foram utilizadas as temperaturas de 1, 2, 3, 4, 5, 6, e 12 horas atrás. A amplitude (temperatura máxima – temperatura mínima) de 1, 2 ,3, 4, 5, 6 e 12 horas atrás. A temperatura mínima ocorrida a 3, 4, 5, 6, e 12 horas atrás. Também foi criada uma correlação linear móvel, que captura a correlação linear entre a temperatura no instante atual com a temperatura de 12 horas atrás.

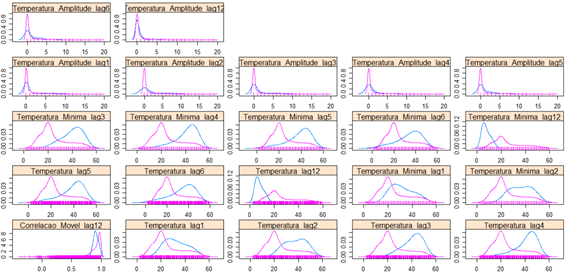
Figura 14 – Densidade das variáveis defasadas (lag) no tempo para temperaturas críticas e não críticas

Para concluir a engenharia de variáveis, foi criada uma variável que vai de 1 até 365, para capturar variação linear das temperaturas ao longo dos dias dos anos.

Ao término da engenharia de variáveis, foram criadas 34 variáveis preditoras. Outras variáveis além das aqui apresentadas também foram criadas, mas não tiveram sucesso em separar os eventos de temperatura crítica dos eventos de temperatura não crítica.

3) Gerando Dados Sintéticos para Classe Minoritária

No aprendizado de máquina e na ciência de dados, geralmente encontramos um termo chamado distribuição de dados desequilibrada, geralmente acontece quando as proporções de observações em uma classe da variável resposta são muito maiores ou menores que as outras classes.

Neste estudo de caso, no período histórico disponível, das 18.572 observações de temperaturas disponíveis (após agregar os dados por hora), dessas, apenas em 138 observações ocorreram temperaturas menor ou igual a seis graus, ou seja, o evento que o algoritmo deve predizer com 12 hora de antecedência que é ‘Ocorrer uma temperatura crítica’, ocorreu em 0,74% do histórico disponível.

Algoritmos de aprendizado de máquina como Árvore de Decisão e Regressão Logística, têm uma tendência para a classe majoritária e tendem a ignorar a classe minoritária. Eles tendem apenas a prever a classe majoritária e, portanto, apresentam grandes erros de classificação da classe minoritária em comparação com a classe majoritária.

Para trabalhar esse desequilíbrio, foi utilizado um algoritmo para gerar dados sintéticos da classe minoritária, chamado SMOTE (Synthetic Minority Oversampling Technique). O objetivo é equilibrar a distribuição de classes aumentando aleatoriamente exemplos de classes minoritárias, replicando-os.

O SMOTE sintetiza novas observações entre as observações existentes da classe minoritária. O algoritmo gera essas novas observações sintéticas por interpolação linear. São gerados pela seleção aleatória de um ou mais vizinhos mais próximos para cada observação na classe minoritária.

O SMOTE funciona da seguinte forma:

Passo 1: Defina o conjunto da classe minoritária A, para cada x ∊ A, os k-vizinhos mais próximos de x são obtidos tomando a distância euclidiana entre x e outra amostra do conjunto A. A distância euclidiana entre dois elementos amostrais pode ser obtida pela fórmula:

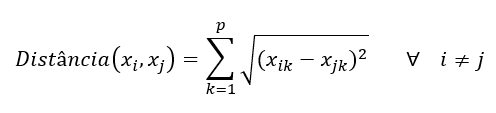
Onde k é o número de variáveis preditoras. Ou seja, a distância entre o par de observações x_i e x_j utilizando a distância euclidiana é raiz quadrada do somatório das diferenças ao quadrado entre cada variável, para todo i diferente de j, pois se calcular a distância da observação com ela mesma, a distância será zero.

Passo 2: Para cada x ∊ A, n elementos amostrais são selecionados aleatoriamente a partir de seus k-vizinhos mais próximos e formam o conjunto A₁.

Passo 3: Para cada elemento amostral contido em A₁, a seguinte fórmula é usada para gerar um novo elemento amostral sintético:

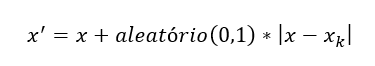
Onde o argumento ‘aleatório’ é um valor contínuo entre zero e um gerado aleatoriamente.

Para apresentar em três dimensões a proporção de elementos amostrais onde ocorreram temperaturas críticas antes e após a aplicação do SMOTE, as variáveis preditoras no conjunto de dados foram combinadas linearmente através dos 3 primeiros autovetores obtidos a partir de sua matriz de covariâncias. Ou seja, sendo X uma matriz contendo as p variáveis preditoras, Σ_pxp a matriz quadrada de covariâncias de ordem p, 𝝺₁≥ 𝝺₂≥ …𝝺_p os autovalores da matriz Σ_pxp , e v_1, v_2,… v_p seus respectivos autovetores normalizados. As três dimensões plotadas nas figuras 15 e 16 são obtidas da seguinte maneira:

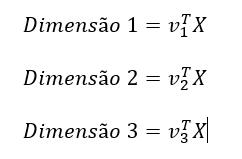
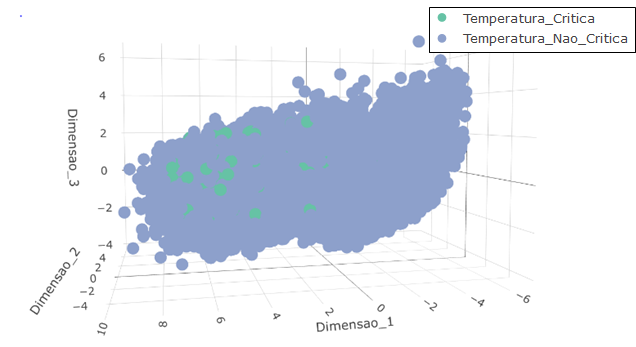
Figura 15 – Apresentação em três dimensões dos dados antes do balanceamento de classes pelo SMOTE

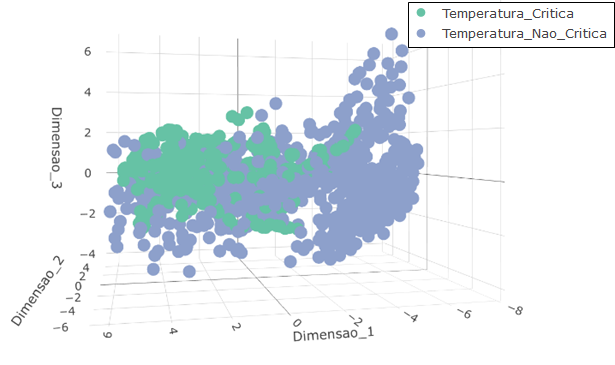
Figura 16 – Apresentação em três dimensões dos dados após o balanceamento de classes pelo SMOTE

4) Regressão Logística

A literatura fornece uma rica variedade de algoritmos de aprendizado de máquina para modelagem preditiva, é esperado que diversos algoritmos sejam ajustados aos dados e aquele que apresentar a melhor capacidade preditiva de acordo com o contexto é escolhido para ser implementado em produção. Neste estudo, o objetivo é apresentar o contexto e como foi solucionado utilizando aprendizado de máquina, e a modelagem preditiva utilizando a Regressão Logística foi a que apresentou melhores resultados. Outros algoritmos também foram testados, incluindo algoritmos baseados em árvores de decisões como o Random Forest e o Gradient Boosting Machine, e algoritmos baseados em funções discriminantes como o Discriminante Linear de Fisher e o Discriminante Quadrático. Porém foge do objetivo do artigo apresentar comparações entre a performance preditiva dos algoritmos, portanto o foco será apenas na Regressão Logística.

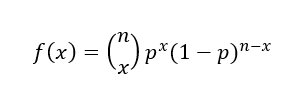
A Regressão Logística faz parte dos modelos lineares generalizados, que é uma variação da regressão de mínimos quadrados ordinários. Portanto, apesar de conter a palavra Regressão em seu nome, a Regressão Logística é utilizada para tarefa de classificação pois é baseada na distribuição binomial, que é utilizada para mensurar a probabilidade de que determinado número de sucesso ocorra em n tentativas. E pode ser representada pela equação:

Onde n é o número de tentativas, x é o número de sucessos e p é a probabilidade de sucesso.

Outro exemplo dos modelos lineares generalizados é a Regressão Poisson e a Regressão Binomial Negativa, que são utilizados para dados de contagem.

A regressão logística modela a probabilidade de uma observação pertencer a uma determinada categoria de saída, que neste contexto, as categorias são 1 = Ocorrerá uma temperatura crítica no trilho em doze horas e 0 = Não ocorrerá uma temperatura crítica no trilho em doze horas.

O modelo de Regressão Logística ajustado tem a forma:

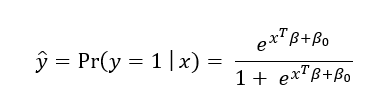
Como alternativa pode ser escrito como:

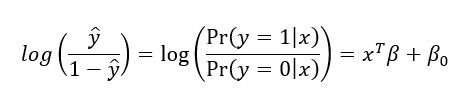
Isso pode ser interpretado como o log da razão de chances do evento a ser predito y = 1 ocorrer dado os valores dos preditores x, pelas chances do evento a ser predito não ocorrer y = 0 dado os valores dos preditores x.

Os coeficientes β da equação são estimados maximizando função de verossimilhança sobre o conjunto de dados históricos:

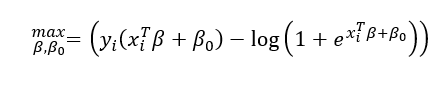
Levando em conta quem os preditores podem ser correlacionados entre si e que nem todos preditores podem contribuir de maneira significativa para a predição, restrições foram adicionadas na função de verossimilhança. Restrições conhecidas como Restrição L₁ (também chamada de Lasso) e a restrição L₂ (também chamada de Ridge). Ao adicionar as duas restrições na função objetivo, o modelo de penalização é chamado de Elastic Net.

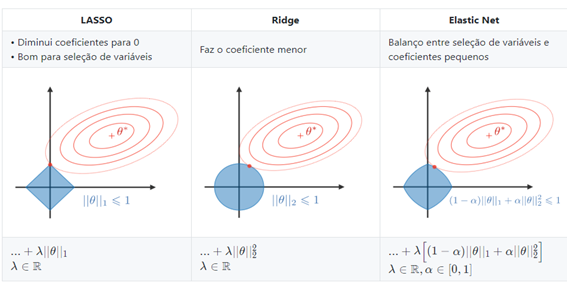
Figura 17 – Restrições L₁ (Lasso), L₂ (Ridge) e L₁ + L₂ (Elastic Net) – Fonte https://stanford.io/2YPUjcz

O valor para a constante α na restrição Elastic Net indica o peso que a restrição L₁ e a L₂ terão sobre a função de verossimilhança, estes podem variar de 0 a 1. Valores abaixo de 0,5 dão maior peso a restrição L₂ e valores acima de 0.5 dão maior peso a restrição L₁. O valor para α deve ser escolhido pelo pesquisador. Uma observação importante é que na figura 17 o autor utilizou a notação θ para representar os coeficientes que nesse artigo estão sendo representados por 𝜷.

O valor para a constante λ (também conhecida como multiplicador de Lagrange) de cada restrição, pode ser estimado via validação cruzada.

No processo de validação cruzada o conjunto de dados é dividido em k partes, um modelo preditivo é ajustado nas k-1 partes, e aplicado na parte que ficou de fora. Esse processo é repetido k vezes e o modelo final é ajustado ao conjunto completo de dados. O erro das predições é então calculado tomando a média aritmética dos erros nos k modelos ajustados.

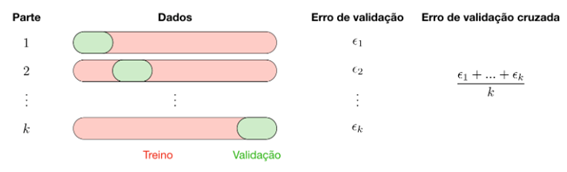
Figura 18 – Processo de Validação Cruzada (k-fold cross validation) – Fonte https://stanford.io/2YPUjcz

O procedimento de adicionar as restrições L₁ e L₂ na função de verossimilhança, que também é chamado de regularização da função de verossimilhança, visa evitar que o modelo super ajuste os dados e seja capaz de lidar com os problemas de alta variância. Um detalhe interessante da restrição L₁ é que automaticamente é feita uma seleção de variáveis, pois o coeficiente β de uma variável preditora que não esteja contribuindo de forma significativa para a predição pode ser ponderado pelo multiplicado pela constante de penalização λ até se tornar igual a zero.

A função de verossimilhança com as restrições fica:

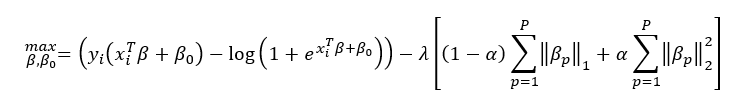
Onde p é a quantidade de preditores.

Muitos pacotes estatísticos utilizam o algoritmo de Newton para otimizar a função de verossimilhança, em um processo chamado de mínimos quadrados reponderados iterativos (IRLS), entretanto, devido a adição das restrições, o método utilizado foi a Descida Coordenada, que se baseia na ideia de otimizar uma função multivariada em uma direção de cada vez. Os passos matemáticos do algoritmo de otimização estão além do escopo do presente artigo mas há bastante literatura disponível.

4) Avaliação da Performance Preditiva do Algoritmo

Uma das formas de avaliar o quão bem ajustado aos dados o algoritmo de aprendizado de máquina está, é aplicar o algoritmo nos próprios dados históricos e comparar a classe real de cada observação com a classe predita pelo algoritmo e obter a taxa de acerto. Entretanto essa abordagem pode gerar uma conclusão enviesada pois o algoritmo já “conhece” os dados em que ele foi ajustado, dados estes que também são chamados de conjunto de treino. Sendo assim, o processo de validação cruzada seria bastante pertinente aqui.

Entretanto, no contexto apresentado, a validação cruzada não será efetiva. Pois o SMOTE foi utilizado para gerar observações sintéticas e equilibrar as classes. Dessa forma a proporção de observações que possuem a temperatura crítica não reflete a realidade. Finalmente, o procedimento utilizando para avaliar a performance preditiva do algoritmo, em dados que ele ainda não “conhece”, foi o chamado Hold-Out. Que consiste em utilizar um percentual do histórico de dados para treinar o algoritmo e separar o percentual restante para validação. Então é avaliada a taxa de acertos do algoritmo nesse conjunto de validação.

No estudado apresentado, os dados são ordenados ao longo tempo, portanto as medições do período de janeiro de 2017 até dezembro de 2018 foram utilizadas para formar o conjunto de treinamento, e as medições de janeiro a março de 2019 utilizadas para formar o conjunto de validação. Importante observar que o SMOTE foi aplicado somente no conjunto de treino, para que no conjunto de validação seja refletida a proporção real entre as ocorrências e não ocorrências de temperaturas críticas.

Para avaliar a taxa de acertos do algoritmo, uma tabela cruzando a coluna da variável resposta original e a variável resposta predita é obtida. Essa tabela leva o nome de matriz de confusão, que é uma tabela que nos informa os erros e acertos de predição do algoritmo. A matriz de confusão é calculada utilizando apenas duas colunas, a variável resposta que já estava no conjunto de dados e uma nova coluna informando a classe que o algoritmo predisse para cada observação. Independente do contexto, sempre que trabalhamos com uma tarefa de classificação, deve ser definida qual será a classe positiva e a negativa da variável resposta. A classe positiva não necessariamente é algo bom, mas é o que se busca predizer com o algoritmo. Neste contexto a classe positiva é “Ocorrer_Temperatura_Crítica”, pois é esse evento que estamos interessado em prever.

                Figura 19 – Estrutura geral da matriz de confusão para um classificador binário

A célula A trará a quantidade de observações da classe positiva que foram preditas como pertencentes da classe positiva. Ou seja, o quanto o algoritmo acertou para a classe positiva (verdadeiro positivo).

A célula B trará a quantidade de observações da classe positiva que foram preditas como pertencentes da classe negativa. Ou seja, o quanto o algoritmo errou para a classe negativa (falso negativo).

A célula C trará a quantidade de observações da classe negativa que foram preditas como pertencentes da classe positiva. Ou seja, o quanto o algoritmo errou para a classe positiva (falso positivo).

A célula D trará a quantidade de observações preditas como pertencentes da classe negativa e que realmente eram da classe negativa. Ou seja, o quanto o algoritmo acertou para a classe negativa (verdadeiro negativo).

Observe que os elementos da diagonal principal da matriz (células A e D) correspondem a quantidade de acertos, e os elementos fora da diagonal principal (células B e C) correspondem aos erros.

O output da regressão logística é uma probabilidade, então um ponto de corte (threshold) deve ser definido, de forma que, se a probabilidade estimada for acima do ponto de corte, a predição será considerada como pertencente ao evento positivo (ocorrerá temperatura crítica), caso contrário, a predição será considerada como pertencente ao evento negativo (não ocorrerá temperatura crítica).

Na literatura existem diversas métricas para orientar o pesquisador a identificar o melhor ponto de corte de acordo com o contexto do experimento.

A princípio a métrica chamada F2 foi considerada, pois é uma métrica que penaliza alta quantidade de falsos negativos, e esse é o erro mais crítico no contexto desse artigo. Pois se o algoritmo predizer que não ocorrerá temperatura crítica no trilho nas próximas doze horas, e ocorrer, os danos podem ser catastróficos. Ou seja, o ponto de corte escolhido deve ser aquele que resulte no maior valor de F2. Seu valor varia entre zero e um e quanto maior melhor. A medida F2 pode ser obtida pela seguinte equação:

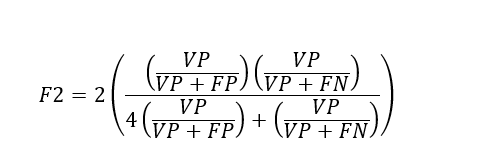
Onde VP são os verdadeiros positivos, FP os falsos positivos e os FN os falsos negativos.

Entretanto, devido ao enorme desbalanceamento entre as classes de interesse no conjunto de dados de validação, essa métrica não foi útil na prática. Finalmente, a métrica adotada foi o Erro Médio por Classes (mean per class error), que consiste em obter um ponto de corte que irá gerar a menor média entre a taxa de erros para classe de interesse e a classe de não interesse. Ou seja, o ponto de corte deve minimizar a seguinte equação:

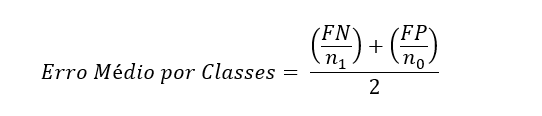
Onde FN são os falsos negativos, FP os falsos positivos, n₁ é a quantidade de observações pertencentes a classe 1, e n₀ é a quantidade de observações pertencentes a classe 0.

ANÁLISE DOS RESULTADOS

Foram testados cem valores para a constante λ de penalização, sendo o valor mínimo λ= 1.881E-4 e valor máximo λ = 0.3525. Para cada valor foi realizado um procedimento de validação cruzada com k=5. Ou seja, foram ajustadas 500 regressões logísticas. O valor de λ que obteve a melhor performance preditiva foi 2.065E-4.

Para o valor de alfa α foi utilizada uma grade de busca (grid search) testando valores de α=0.0 até α=1.0, incrementando de 0.1. O melhor valor foi α=0.99, que é basicamente uma regressão L₁ (lasso).

 O algoritmo de Descida Coordenada gastou 163 interações para otimizar a função objetivo.

O modelo iniciou com 32 preditores e finalizou com 24 preditores. Ou seja, a restrição L₁ zerou o coeficiente de algumas das variáveis.

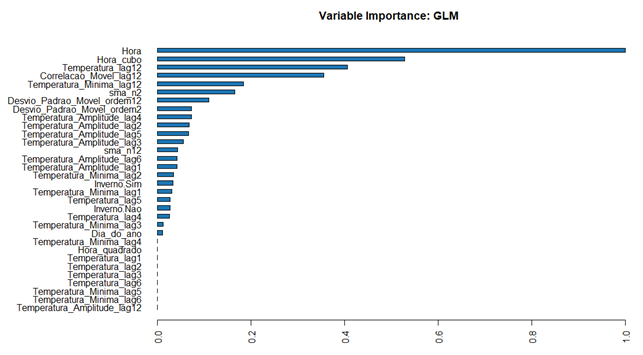
        Figura 20 – Variáveis consideradas mais importantes pelo algoritmo

Na figura 20 pode-se visualizar as variáveis que o algoritmo considerou mais importante para predição. As variáveis Hora, Hora ao cubo e a temperatura de 12 horas atrás (lag 12) foram as três variáveis mais importantes. E as variáveis partir Temperatura Mínima Lag4 foram removidas do modelo pela restrição L₁ .

Na figura 21 pode-se visualizar a matriz de confusão na amostra de validação, utilizando o ponto de corte de 49%.

                                Figura 21 – Matriz de confusão na base de validação

Das 28 observações que ocorreram temperaturas críticas, 27 o algoritmo acertou e 1 ele errou (falso negativo). Houveram 231 falsos positivos, que são alarmes falsos, mas que são menos custosos e mais administráveis que os falsos negativos.

CONCLUSÕES

Após todos os experimentos científicos com os dados e algoritmos foi possível compreender que é possível utilizar aprendizado de máquina para predizer com doze horas de antecedência com uma taxa de acerto bastante interessante. Como próximos passos, está prevista a expansão desse conceito de modelagem preditiva a outros termômetros em outros corredores logísticos. Pois o algoritmo ajustado “aprendeu” os padrões nas temperaturas para esse termômetro, em outros, o comportamento da temperatura será diferente, portanto um novo modelo preditivo deve ser ajustado aos dados.

REFERÊNCIAS BIBLIOGRÁFICAS

BOLDRINI, Costa; WETZLER, Figueiredo. Álgebra Linear. 3. ed. São Paulo: HARBRA, 1986.

CHAWLA, N. V., BOWYER, K. W., Hall, L. O., and KEGELMEYER, W. P. (2002). Smote: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 16:321-357.

GUJARATI, Damodar N.; PORTER, Dawn C.. Econometria Básica. Tradução de Denise Durante et al. 5. ed. Porto Alegra: AMGH Editora Ltda., 2011.

HASTIE, Trevor et al. An Introduction to Statistical Learning: with Applications in R. 1. ed. New York: Springer, 2013.

HASTIE, Trevor; TIBSHIRANI, Robert; FRIEDMAN, Jerome. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2. ed. New York: Springer, 2009.

MINGOTI, Sueli Aparecida. Análise de Dados Através de Métodos de Estatística Multivariada: Uma Abordagem Aplicada. 1. ed. Belo Horizonte: Editora UFMG, 2005.

Mineração de Dados – Página 106 de 106

TORGO, L. (2010) Data Mining using R: learning with case studies, CRC Press (ISBN: 9781439810187)

#Aprendizadodemaquina #machinelearning #estatistica #previsao #cienciadedados

Linkedin Prof. Máiron Chaves:

https://www.linkedin.com/in/maironchaves/

Playlist Prof. Mairon Chaves Estatidados: